- LPCNet: Improving neural speech synthesis through linear prediction
- https://arxiv.org/abs/1810.11846
LPCNet 是 WaveRNN 的一种变体,将线性预测 LP 与 RNN 网络相结合,显著提高了语音合成的效率。当网络大小相同时,LPCNet能达到明显更高的合成品质,而且计算复杂度更低,能够更简便的应用于嵌入式/移动端等低功率设备。
前人的 WaveNet 工作要求在高端GPU机器上才能达到实时,WaveRNN对算力要求有所降低但仍然代价较大,论文在WaveRNN的基础上进一步研究。
| While they are generally efficient at modeling the spectral envelope (vocal tract response) of the speech using linear prediction, no such simple model exists for the excitation. Despite some advances [10, 11, 12], modeling the excitation signal has remained a challenge. |
|---|
低比特率声码器在用线性预测 LP 建模语音谱包络时很高效,但是对于激励 (excitation) 信号的建模仍然是个难题。论文提出的 LPCNet 将谱包络预测从神经网络中移除,从而让模型能够更好地用来建模激励,这样传统+新模型结合的方式能够够有效降低模型复杂度。
LPCNet 结构
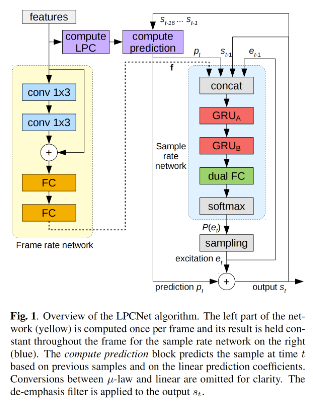
LPCNet 的结构主体包含两个部分,采样率下工作的 sample rate 网络和帧级别工作下的 frame rate 网络。对于 16k 的语音合成任务来说,sample rate 网络工作在 16kHz 下,每秒 16000 个时间步,而 frame rate 网络是每 10ms 帧移一个时间步 (10ms对应160个采样点)。
LPCNet 的输入为 20 维的特征,18 维 BFCC,2 维 pitch (周期和相关系数)。对于低比特率的语音编码任务,BFCC和pitch 参数都可以量化,对于语音合成任务,推理时通常从文本层面先用声学模型预测 20 维特征。
1. conditioning 参数
LPCNet 20维的输入是帧级别的特征,送入的是 frame rate 网络。经过两层 1 * 3 的卷积后,感受野为 [-2, 2],卷积层的输出和原始的 20 维输入特征进行残差连接,经过两层全连接层,输出128维的 conditioning 向量 f 送入 sample rate 网络。对于每帧 160 个采样点,conditioning 向量 f 只计算了一次,是保持不变的。
2. 预加重和量化
WaveNet 的预测目标是 8-bit 的 μ-law 之后的值,这样可能的值只有 2 的 8 次方= 256个值。频谱的能量通常集中在低频,μ-law 的量化噪声在高频更明显,尤其是 16kHz 语音有更高的频谱倾斜。为了解决这个问题 WaveRNN 将输出保留为原始的 16-bit。
LPCNet 针对这一问题采用的方案是仍然使用 8-bit 的 μ-law。对于训练数据的预测值,先使用预加重,相当于预测的是预加重之后的结果;对于预测时,再使用与预加重相反的去加重滤波器。实际上相当于人为设计对预测的label 进行了处理。预加重系数为 0.85。
3. 线性预测
语音合成建模了:声门脉冲、噪声激励、声道响应。声道响应可以用全极点线性滤波器来表示。线性预测的思想:在一帧范围内,用当前时刻之前的M个历史信号的线性加权来表示当前的信号,不同历史信号的权重即为线性预测系数 LPC。
线性预测系数的计算方法:
先将 18 个频带的 Bark 频率倒谱 (18 维的 BFCC) 转换为 Bark 频率的功率谱密度 PSD,然后用 iFFT 转换为自相关,使用 Levinson-Durbin 算法可以从自相关中计算出 predictor。
事实上,从倒谱进行 LPC 分析不如直接从信号计算的精确,但是影响不大因为网络对这部分预测的损失学习进行补偿 (因为预测的label来源是实际的语音信号)。
另外,与直接预测采样点的数值相比,预测 [residual] 采样点之间的差是一个更简单的任务,而且残差的数值范围明显比预加重之后采样值的范围小,所以 μ-law 的量化误差也能有所减少。
总结:是上一时刻的参数e,上一时刻的信号s 以及当前的预测 p。不仅有残差还有信号本身,因为论文发现如果只使用残差 e,语音质量不行。
4. 输出层
论文在输出层上用的是 Dual FC,相当于输入经过两个单独的 FC 之后,再分别与一个可训练的向量逐元素相乘后相加。这个 Dual FC 不是完全有必要,但是论文发现这种结构下能够略微提高合成质量。
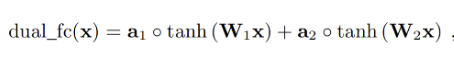
论文解释 Dual FC 有效的原因:对于μ-law量化来说,决定采样值落入哪个区间范围,需要两次比较,也就是量化区间的左右边界各需要比较一次,但是一个FC只能带来一次比较。(不理解此处的FC输出如何与量化联系起来?) Dual FC 的输出经过 softmax 之后预测的是 et 残差的概率分布。
5. 稀疏化矩阵
LPCNet 结构中包含 GRU_A 和 GRU_B 两个 GRU。GRU_A的模型参数量最大,论文采用的稀疏化训练方式和WaveRNN一致。但是,LPCNet会在系数矩阵中保留对角元素,向量化计算起来也比较简便,只是element-wise的乘法运算。
6. embedding 和代数简化
论文没有将采样值映射到一个固定的区间,而是利用了μ-law的离散特性来学习一个 embedding 矩阵。embedding可以将μ-law 的等级映射为向量,从而学习到一系列非线性方程,能够将μ-law刻度转换到线性刻度。
代数简化后,embedding可以直接从一次性计算的矩阵中lookup得到;每帧 160 个采样点,也只需要计算一次 conditioning 向量进入 GRU 之后的结果。
对于 GRU_B,没有采用稀疏化训练,就是普通的GRU + 全连接 + ReLU 即可。
7. 如果从概率分布采样
直接从输入概率分布采样可能造成噪声,引入常数c来控制采样。论文设置了阈值,避免概率值过低造成的冲激噪声?P(et) 概率分布先进行指数c的规整,然后基于R操作得到均匀分布,设置阈值
T = 0.002,最终还有个均匀分布的规整。

8. 训练的噪声注入
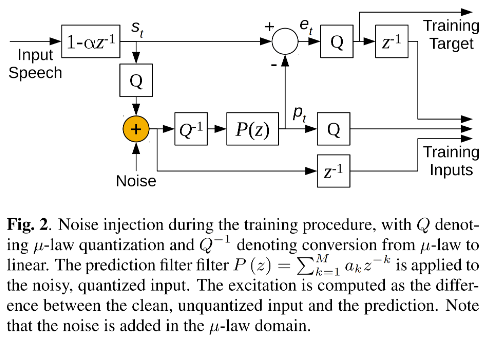
对于这种序列生成的任务,普遍有训练和推理时不匹配的问题。训练时使用的是采样点比推理时生成的采样点更好。不匹配的问题在推理时会造成失真。为了让模型在推理时更加鲁棒,需要在训练时进行噪声注入。
在线性预测时,噪声注入的细节很关键。不是在 input speech信号上注入噪声,也不是在预加重之后的采样点上,而是在 μ-law 量化之后。量化之后注入噪声再反量化返回到线性刻度,然后再用 P(z) 的 LP 预测。噪声值采用的是均匀分布。
实验与评测
1. 计算复杂度
每个采样点的计算量:
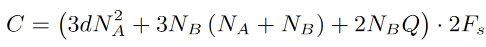
d 是 GRU_A 的非系数程度,N_A N_B 分别是GRU_A 和B的隐含结点数,Q 是μ-law值的可能的个数(256),Fs是采样率。公式中还有一些激活/bias没有体现。总共的计算量是 2.8 GFLOPS,可以在移动端达到实时。
WaveNet 是 16 GFLOPS,WaveRNN 是 10 GFLOPS,SampleRNN是50 GFLOPS。
2. 实验配置
特征直接从语音中提取。频带划分:
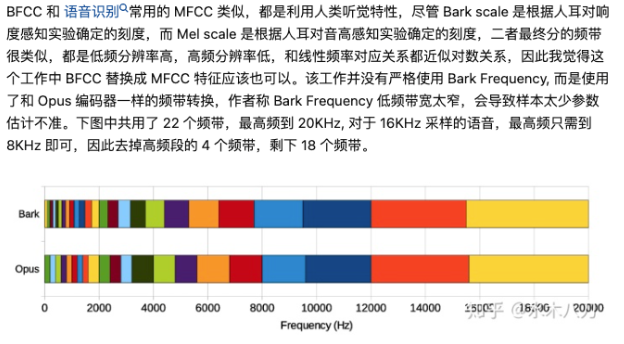
| 为了避免过高的计算复杂度,假设语音和噪声的频谱足够平坦,以使用较粗的频率分辨率。与其它一些方法直接估计谱幅度不同,文章直接估计理想临界带的增益,其取值范围在0到1之间。将频谱以类似于 Bark scale 的尺度进行划分,也就是说在高频部分,带的划分和Bark scale一样,但在低频部分,至少有4个频点。文章使用三角形带,并且峰值响应位于相邻带的边界。这样总共会产生22个带,因此,只需输出22个位于0和1之间的值即可。 |
|---|
基频估计:open-loop cross-correlation search
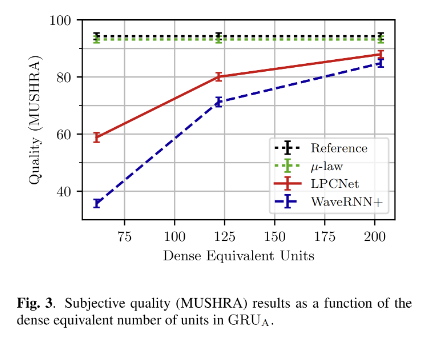
实验结果对比,LPCNet 明显优化 WaveRNN+,WaveRNN+ 是 WaveRNN的优化版,除了用LPCNet 来预测 pt 以外,其他的优化都用在 WaveRNN 上。
摘选大佬的理解
类比 source-filter 模型, 全神经网络的做法既要让 NN 建模 source 又要建模 filter 很难也很浪费,因为 filter 部分用 DSP 实现其实非常简洁高效,有经典的 Levinson-Durbin 算法,但是使用 NN 实现却可能非常复杂。
以 WaveRNN 为基础显式加入 LPC filter 模块来降低神经网络部分的复杂度。一个直觉的想法是 WaveRNN 需要为整个采样值建模,那么如果将这个采样值分解成线性和非线性两部分,线性部分通过基于 DSP 的线性预测给出,神经网络仅需建模变化相对较小的非线性残余部分,这会是个更简单的任务,更少的神经元便可以胜任。
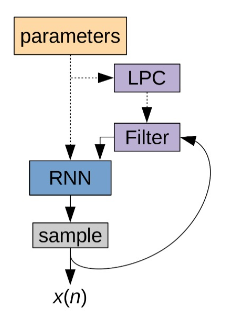
LPC 计算模块则从输入特征中计算线性预测参数 LPC,LPC 是一帧计算一次,并在帧内保持不变。

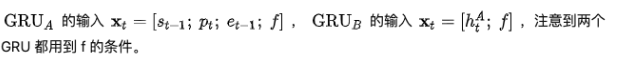
- 本文标题:声码器 | LPCNet:基于线性预测的声码器
- 创建时间:2022-06-08
- 本文链接:2022/06/08/2022-06-08_lpcnet/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
