专题分享 | GAN 系列之三：最小二乘 GAN

• Least Squares Generative Adversarial Networks
• ICCV 2017 pdf

本文实际上是对原始 GAN 论文的改进，主要从 GAN 的损失函数角度进行了改进，将 GAN 的判别器的损失函数从 sigmoid 交叉熵，修改为了回归模型使用最小平方误差。改进虽小，但是效果很好，后续 TTS 领域基于 GAN 的声码器，不少都是在 LS-GAN 的基础上进行的工作。

原始 GAN 工作的缺点：判别器使用交叉熵损失函数指导训练，可能会导致梯度消失问题。采用最小平方损失函数相当于最小化 Pearson 卡方散度。LS-GAN 相比于普通 GAN 的优势：

1. 结果上：在图像生成任务上，能够生成比普通 GAN 更高质量的图片

2. LS-GAN 的训练过程相比于普通 GAN 更加稳定

LS-GAN 的可行性解释：交叉熵损失函数是分类 loss，只关注比较硬的 label，对于分类正确的样本，不管这些样本距离分类界面多远，损失函数都是0，所以不会对反向传播时的参数更新产生影响。但是最小平方误差相当于使用了软 label 的回归任务，这样对于距离分类界面远的样本，会进行相应的惩罚，使得判别器的分类界面相比于原始的 GAN 会更精准，反之会促进生成器生成的样本和真实样本更接近。不使用分类的硬 label 计算损失函数，也会使得损失函数计算来源更广，梯度计算和参数更新会代入更丰富的信息，使得 GAN 的训练更加稳定。

LS-GAN 的理论分析

原始 GAN 的 minimax 目标函数：

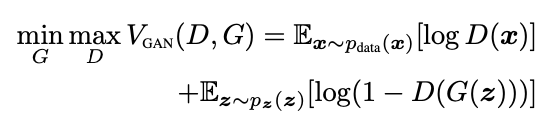
GAN 的训练过程分为优化判别器 D 和优化生成器 G 两部分：

1. 优化判别器

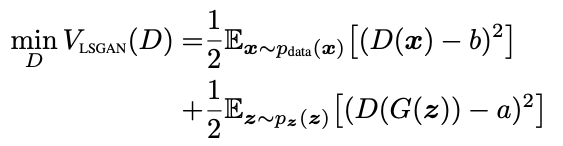
2. 优化生成器

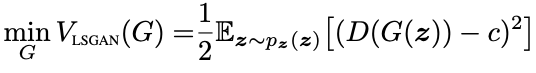
简单理解，对于原始的普通 GAN，一般 a = 0, b = 1, c = 1。分别表示：生成的样本应该判别为 0，真实的样本应该判别为 1。但是论文进行了扩展，a、b 分别表示生成样本和真实样本对应的数值；c 表示生成器希望判别器将生成样本判断成什么数值。

同样地，按照 GAN 原始论文的推导方法，可以将最小平方 GAN 的目标函数进行最优解求解。先固定生成器 G，计算判别器 D 的最优解为：

将最优的 D 代入 G 的目标函数，可以得到：

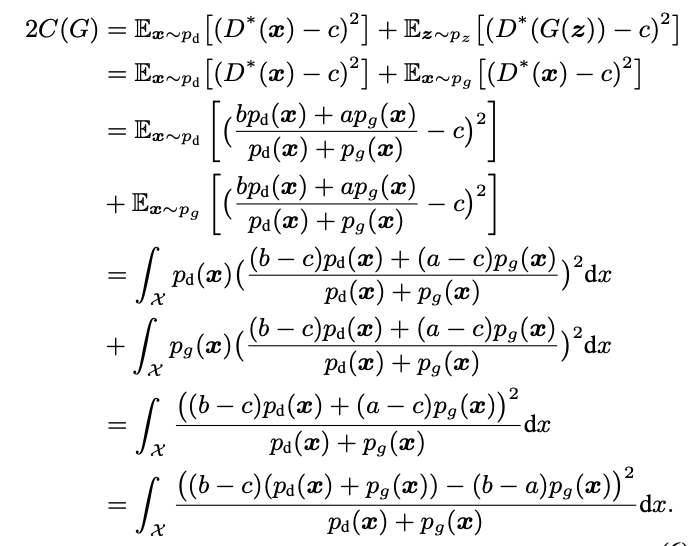
根据上述形式，指定特殊数值时，G 相当于优化一个 pearson 卡方散度

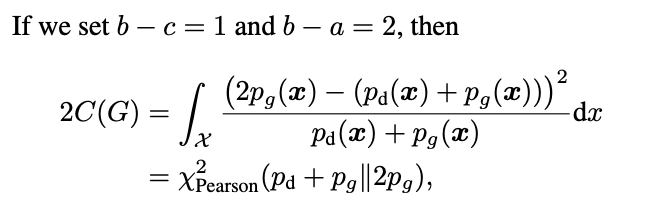
LS-GAN 的参数选择

选项一：a = -1, b = 1, c = 0，此时 G 的最优解是在优化皮尔逊卡方散度

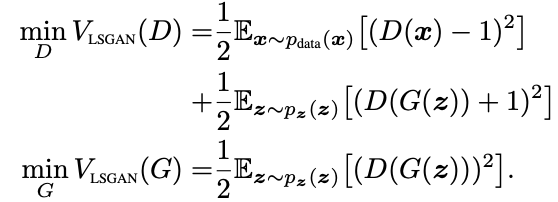
选项二：选项一的 a, b, c 没有太明显的物理含义，所以可以指定 b = c = 1, a = 0，就和生成样本属于0、真实样本属于 1 的实际意义相对应起来，此时优化目标函数为：

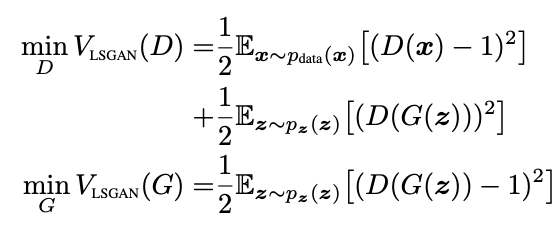
选项一和选项二两种赋值在实际使用时效果差不多，但是之后基于 GAN 的声码器论文中，都是使用的选项二，因此选项二是非常重要的公式。

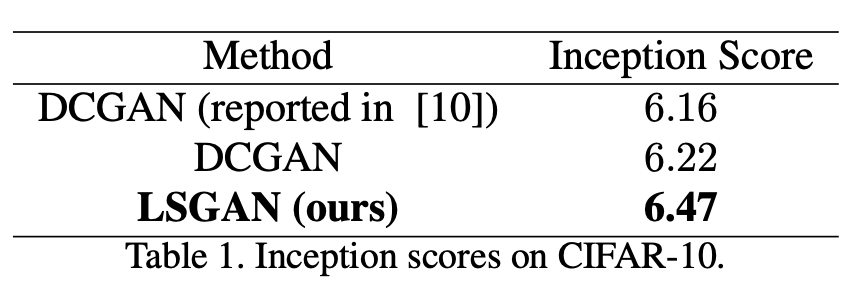
实验结果对比